Ikke les for mye ut av små datagrunnlag
Sist oppdatert:Snarveien: Varselbjellene bør ringe hvis det er de minste avdelingene som topper statistikken. Her er en metode for å ikke la deg lure.
Vi vil så gjerne fortelle en meningsfull historie om det vi ser. Men om du hører deg selv si: «De små kontorene våre er tydeligvis de beste» bør du stoppe opp.
Det kan være at dette bare er et eksempel på de små talls lov.
Små utvalg har større spredning i tallene, og du vil derfor finne dem både i toppen og bunnen av rangeringene. Det er helt normalt, men ikke fall for fristelsen til å fortelle en historie om dem.
Eksempel: Foreldreundersøkelsen
For noen år siden hadde Fædrelandsvennen en artikkel om foreldreundersøkelsen for barnehagene i Agder. Ikke overraskende kom en av de minste barnehagene godt ut av spørreundersøkelsen:
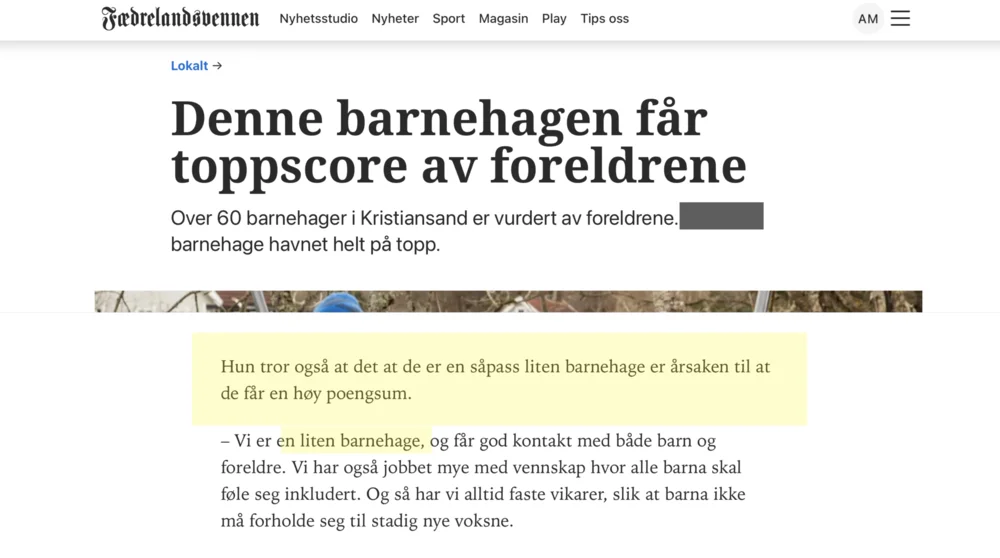
Kanksje er det, som styreren sier, at barnehagen faktisk er bedre siden den er liten. Men det er også en fare for at det kun er en narrativ feilslutning – at vi forteller en historie om noe som ikke er der.
Ifølge de små talls lov kan vi forvente å finne de minste barnehagene både i topp og bunn av statistikken.
Slik ser det ut når vi plotter resultatene fra foreldreundersøkelsen på y-aksen og antall respondenter på x-aksen:
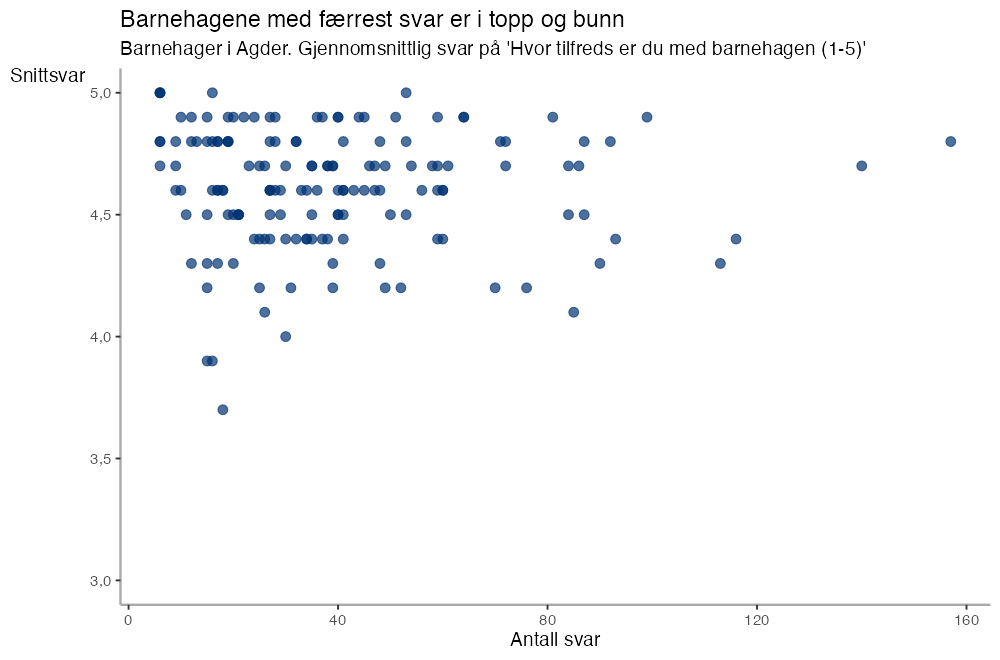
Barnehagen i artikkelen er helt oppe i venstre hjørne. Det kan være en velfortjent skår, men den er mer påvirket av tilfeldig variasjon enn barnehagene med flere svar.
Se etter en traktform
Hvis variasjonen faller når utvalget blir større, vil grafen ha en form som en trakt.
Etter hvert som antallet i utvalget øker, blir variasjonen mindre.
Du ser det ofte i medisinske data, som i denne grafen om tarmkreft i Storbritannia fra Paul B.
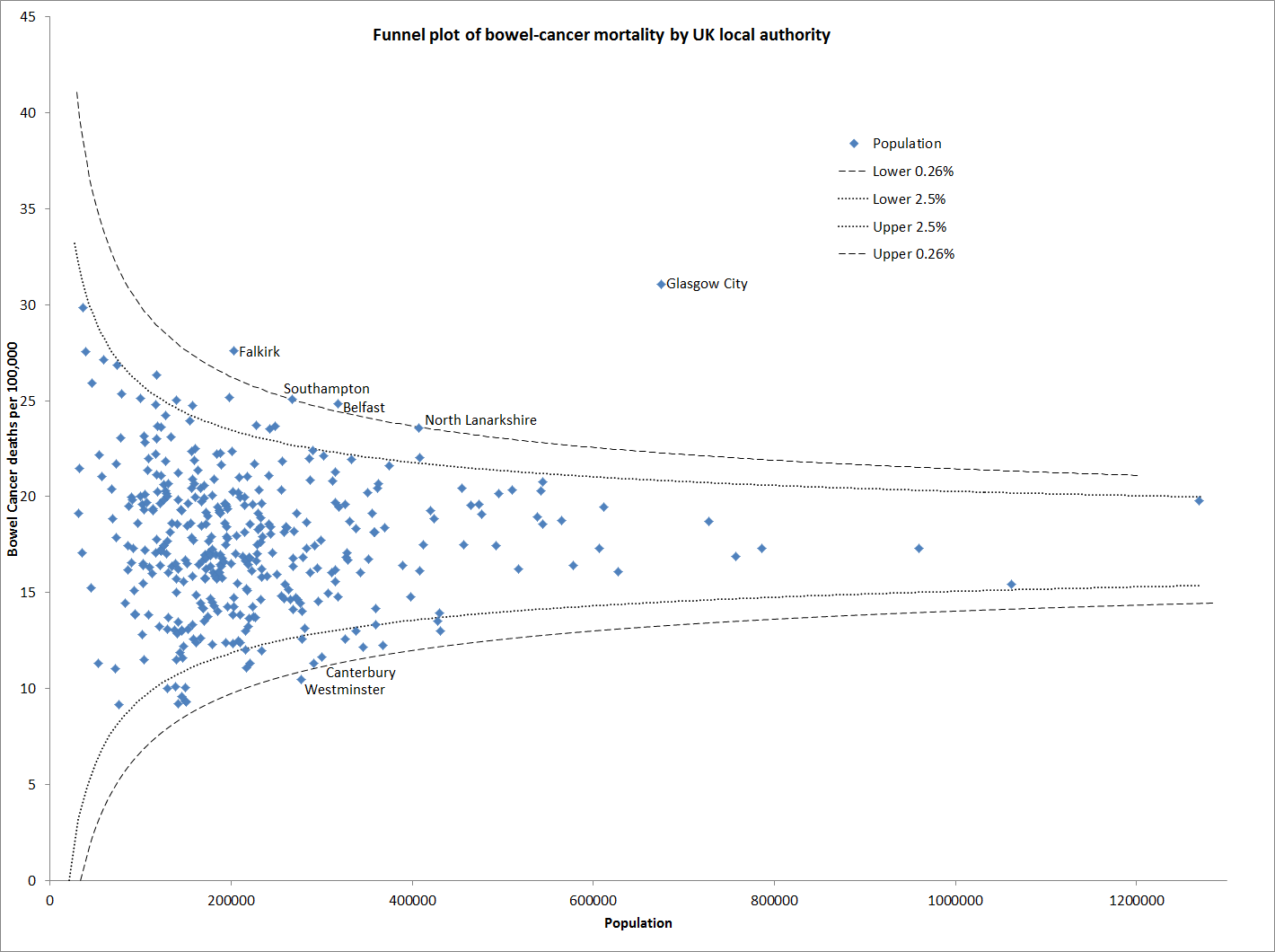
Selv om det hadde vært fristende å skrive at regionene helt til venstre har unormalt høy eller lav dødelighet, er det ikke nødvendigvis riktig, siden de har minst befolkning. Det er mer hold for å si at Glasgow har unormalt høy dødelighet. De har en større befolkning, og dermed mindre tilfeldig variasjon.
Hva kan du gjøre?
Det viktigste du kan gjøre er å se på små utvalg med sunn skepsis. Ikke hopp til konklusjonen at små steder er noe bedre eller verre enn større.
En annen enkel løsning er å bare se bort fra de minste utvalgene. Da overtolker du det i alle fall ikke. Men du går glipp av data, så en bedre å måte er å bruke et triks fra den gode pastor Thomas Bayes:
Bayesiansk gjennomsnitt
Legg til 10 foreldre som er helt OK fornøyde til hver av barnehagene.
Det vil trekke skåren i retning av gjennomsnittet, men effekten vil bli størst på de små utvalgene. For de små barnehagene vil det trekke skåren kraftig mot gjennomsnittet. De største vil ikke bli så påvirket.
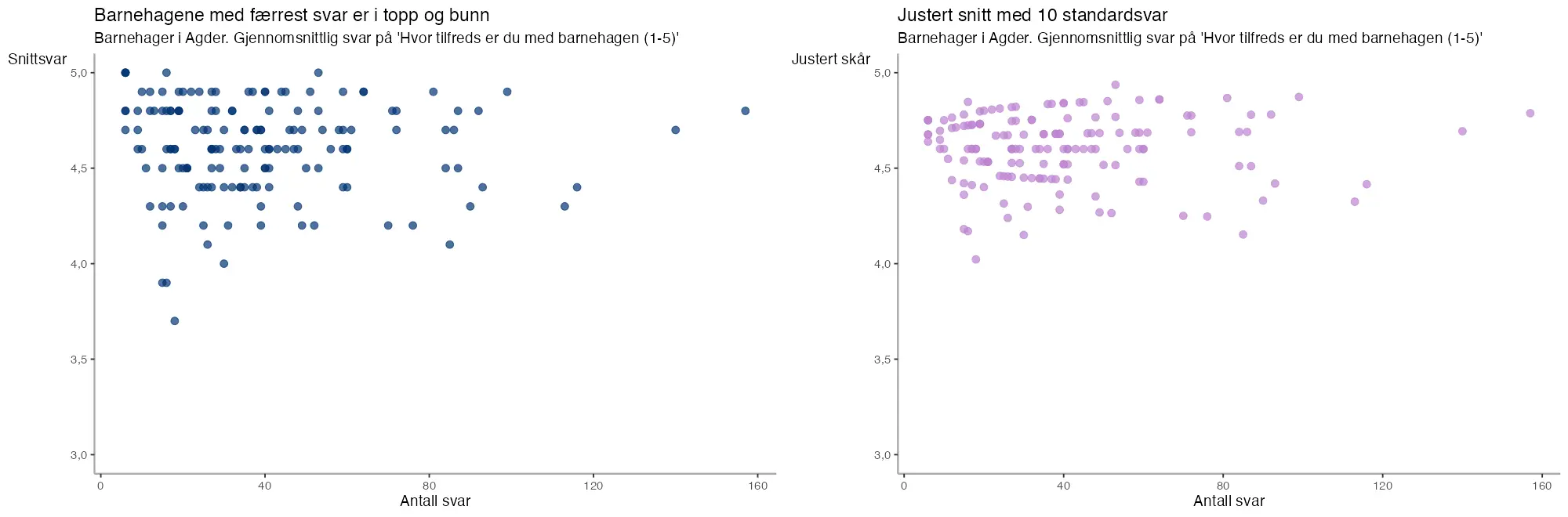
Tanken bak er enkel: Ekstraordinære resultater krever ekstraordinære bevis.
Og i fravær av ekstraordinære bevis må vi starte med å anta at alle er gjennomsnittlige. Derfor legger vi til en gruppe med standardsvar.
Eksempel: Bokanmeldelser
Nettbutikker og rangeringssider bruker enten Bayesiansk gjennomsnitt eller mer sofistikerte metoder.
For å illustrere med et eksempel: Si at du har fått én anmeldelse på fem stjerner for en bok📕. Den andre boken📗 har fått 50 anmeldelser på i snitt 4,7.
Legg til 10 svar til begge på 4 stjerner (vi antar at det er gjennomsnittet for alle bøker). Da får du en utjevnet skår som er mye nærmere snittet for 📕 og bare litt nærmere for 📗:
| 📕 | 📗 | |
|---|---|---|
| Skår | 5,0 | 4,7 |
| Antall | 1 | 50 |
| + Standardskår | 4,0 x 10 | 4,0 x 10 |
| = Justert skår | 4,1 | 4,6 |

Oppsummert
Vær på vakt når du ser ekstraordinære resultater fra små utvalg.
Du kan se helt bort fra dem, men da går du glipp av data.
Hvis du vil ha dem med, kan du vekte gjennomsnittet slik at de minste avdelingene ikke slår ut så hardt.
Kilder og inspirasjon
Denne artikkelen er inspirert av Gaute Hovtuns innlegg på LinkedIn om lottomillionærer i Verdalen.
Det endte med at vi skrev hvert våre nye innlegg om de små talls lov:
For ordens skyld: Grafene er fra 2023-undersøkelsen, og avisartikkelen er fra 2022. De illustrerer likevel de små talls lov.